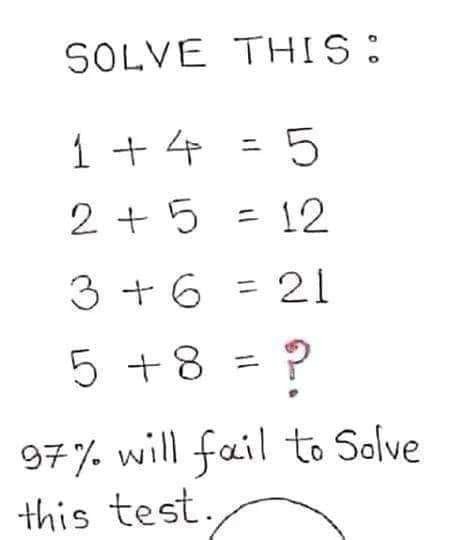If you’re like me, you probably feel grateful that the last time you had to deal with a tricky math problem was back in your school days. Math can be a polarizing subject; some people are drawn to its exactness and logic, while others, like myself, lean towards more creative endeavors. But, as the saying goes, it takes all sorts to make the world go round.

Despite my lack of enthusiasm for math during my school years, I’ve come to enjoy solving puzzles and problems online. Taking my time to figure out these brain-teasers at my own pace is quite satisfying. It seems I’m not alone in this, as many others also take pleasure in tackling challenging math problems for fun.

That’s why we’ve decided to challenge our readers with a math problem that has left many scratching their heads. Ready to give your math skills a workout? Here’s the puzzle for you:

If 1+4=5, 2+5=12, and 3+6=21, then what is the value of 5+8?

It’s clearer to look at it like this:

1+4=52+5=123+6=215+8=?

This puzzle has baffled many internet users, and opinions vary on what the correct answer is. The solution depends on the method you choose to solve it, and interestingly, there is more than just one correct answer! Below are five possible approaches to solve this intriguing math riddle:

Solution one

1 + 4 = 52 + 5 = 2 + 2(5) = 123 + 6 = 3 + 3(6) = 215 + 8 = 5 + 5(8) = 45ALGORITHM: A + A(B) = CANSWER = 45

Solution two

1 + 4 = 1 + 4 + (0) = 52 + 5 = 2 + 5 + (5) = 123 + 6 = 3 + 6 + (12) = 215 + 8 = 5 + 8 + (21) = 34ALGORITHM: A + B + C’ = C, where C’ is the previous answerANSWER = 34

Solution Three

1 + 4 = 5 = 52 + 5 = (5 + 2) + (5) = 123 + 6 = (7 + 2) + (12) = 215 + 8 = (9 + 2) + (21) = 32ALGORITHM: for {X=5, C = X + C’ , X = X+2 };, where C’ is the previous answer. A and B not used in equation,ANSWER = 32

Solution Four

1 + 4 = 52 + 5 = 7 (base 5) =123 + 6 = 9 (base 4) = 215 + 8 = 13 (base 3) = 111ALGORITHM: for {X=6, C = (A + B)^(10 -> X), X -1} (First answer in Base6, then Base 5, then 4, etc…)ANSWER = 111

Solution Five

1 + 4 = 52 + 5 = 7 (base 5) =123 + 6 = 9 (base 4) = 214 + 7 = 11 (base 3) = 1025 + 8 = 13 (base 2) (aka binary) = 1101ALGORITHM: for {X=6, C = (A + B)^(10 -> X), X -1} (First answer in Base6, thenBase 5, then 4, etc…including “missing” numbersANSWER = 1101

What answer did you come up with? Did it match any of these solutions? Feel free to discuss in the comments!